Dingfeng Capacitor--Factors Affecting Value of Capacitance
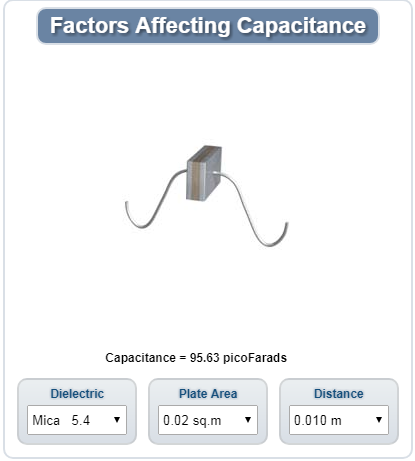
The capacitance of a capacitor is affected by three factors:
- The area of the plates
- The distance between the plates
- The dielectric constant of the material between the plates
Large plates provide a greater capacity to store charge. Therefore, as the plate area increases, the capacitance increases.
The capacitance is proportional to the electrostatic field between plates. When the plate gets closer, the magnetic field is stronger. Therefore, as the distance between plates decreases, capacitance increases. When the distance between plates increases, the capacitance decreases.
As discussed above, the ability of the medium to support electrostatic forces is proportional to the dielectric constant. Therefore, as the dielectric constant increases, the capacitance increases.
Considering the above three factors, the capacitance value of two parallel plate capacitors can be calculated by the formula:
C = (8.855KA) ÷ d
Where C is capacitance in picofarads, K is the dielectric constant, A is the area of one plate in m2, and d is the distance between plates in m.


 info@dfcapacitor.com
info@dfcapacitor.com